组合数学是数数的艺术。

问题一：棋盘的完美覆盖

对于一个 的棋盘，能否用 的长方形骨牌进行不重叠、不遗漏的完全覆盖？

结论是，能完美覆盖的充分必要条件是 或

充分性的证明：即证明若 或 ，则可以完美覆盖。这是显然的，不妨设棋盘是 行 列且 那么将所有长方形骨牌竖着填充即可。

必要性的证明：若棋盘能被完美覆盖，则 或 .

利用染色进行证明。设每一个 的长方型骨牌的每一格上有不同的颜色，则整个棋盘上每一种颜色的格子数目一定是相等的。在 的正方形棋盘中，考虑如下的颜色排列

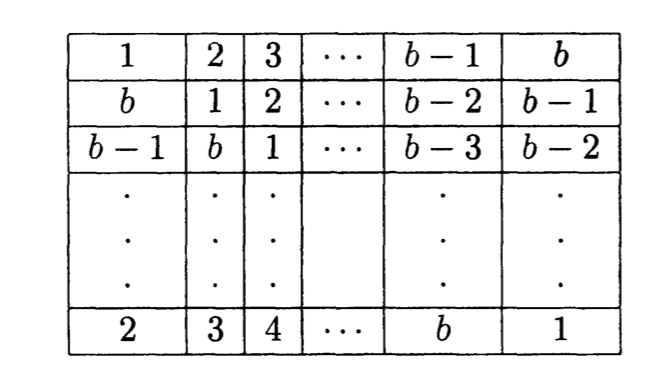
我们以这个 的棋盘为基础，进行填补 的棋盘。为了方便我们不妨令 . 由带余除法知 于是把 的棋盘分为三个部分：上方的 的棋盘，左下方的 的棋盘和右下方的 棋盘。

待补充。

问题二：空间划分问题（1）

给定 条简单曲线（曲线可闭合，但不允许打结），求出这 条曲线最多能将平面划分为多少个区域。

对于可任意弯曲的曲线，我们能得到的区域数的最大值为 即确保增加的第 条曲线 可以经过前 条曲线将平面分成的每一个区域，这样区域数呈指数增加，公比为 下面我们考虑几种特殊的情况：直线与一些二次曲线，分析的基本思路是相同的。

直线

增加的第 条直线需要被前 条直线分为 个部分，而这 条射线或线段经过前 条直线分割成的 个区域区域中的 个区域，并将其分成两份，于是容易得到递推公式为 因此

圆

两个圆最多有两个交点。对于第 个圆 ，它与前 个圆的每一个都有两个交点，于是一共有 个交点。这 个点把圆 分成了 段圆弧，而每一段圆弧都经过前 个圆分割成的若干区域区域中的 个区域，并将其分成两份 ，因此 于是

椭圆

两个椭圆最多有 个交点，将椭圆分为 段。对于第 个椭圆 它与前 个椭圆有 个交点，这些交点把 分成了 条曲线段。在这 条曲线段中，有四条特殊的曲线段，将它们分为两组，其中一组同时经过了最外围的区域，另一组同时经过了最里面的区域（这只是其中一种较为容易分析的一种画法）。对于另外 的曲线段，它们都经过了前 个椭圆分割成的若干区域区域中的 个区域，并将其分成两份，于是 因此

抛物线

两条抛物线最多可以有 个交点，将抛物线分为 段。对于第 条抛物线 它与前 个椭圆有 个交点，这些交点把 分成了 条曲线段。在这 条曲线段中，有 条特殊的曲线段，其中三条同时经过了某个所有抛物线顶点附近的无界区域，另外两条同时经过了最里面的区域（这只是其中一种较为容易分析的一种画法）。对于另外 的曲线段，它们都经过了前 个椭圆分割成的若干区域区域中的 个区域，并将其分成两份，于是 于是

直线和圆

待补充。

三维时的情形

平面

第 个平面 与前 个平面有 条交线，根据已有的二维时的情况，这些交线最多把 分成了 个区域，而这些区域经过了前 个平面分割成的若干区域中的 个区域，并将其分成两份。于是 于是

维的情形

求解三维时，我们很容易注意到不同维度之间存在着递推关系。设 个超平面最多可以将 划分为 个区域。则显然有 维的空间被 个超平面分成的区域数量最多是

归纳易证。在后续文章会再次介绍此数列。

排列与组合

排列

元素集合 的 排列的意思是， 个元素中的 个元素的有序放置。比如集合 的 排列为 我们将 元素集合的 排列的数目记作 显然有 这在高中的记号是 也可以理解为，在 元素集合中选择 个元素，并将这 个元素进行全排列。

圆排列

上面介绍的排列是线性排列。圆排列又称为循环排列，即将取出的 个元素排列成一个圆。 元素集合的 圆排列的数目为 这很容易理解，只需要考察下面 个线性排列： 它们实际上是同一个圆排列，这一共是 个，于是可以将 个线性排列划分为 个部分，每一部分是一个圆排列，因此将线性排列的个数除以 即得圆排列的个数。

组合

元素集合 的一个组合或子集表示集合 的元素的一个无序选择，这是与排列不同的地方。 元素集合 的 子集的意思是它的含有 个元素的子集的集合。用 表示 元素集合的 子集个数，并且有下面的定理

定理1 PROOF 借助排列是十分容易证明的，这是因为由乘法原理显然有

定理2（组合数的性质）

（1）

PROOF 我们可以在 元素集合的 子集的构成的集合与 元素集合的 子集构成的集合之间建立双射，于是等式便得证。

（2）（Pascal公式）

PROOF 在组合数学中，我们更倾向于用组合的方法进行证明。

设 元素集合 满足 的所有 子集的集合记作 并将其划分为两部分 和 其中 中的每个集合都含有 而 中的每个集合均不含，那么显然有 而 等于集合 的 子集的个数， 等于集合 的 子集的个数，也即 这就是要证的。

（3） 这个很容易理解，因为左边的和式相当于 元素集合 所有子集的数目，也即

多重集合

所谓多重集合，就是允许元素重复的集合，比如构成串 的元素可以表示为集合 若元素 有无穷多则可记作

多重集合的排列

定理3 设多重集合 有 种不同的元素，且每种元素的数目分别为 并记 那么 的排列数目为 PROOF 分别在 个位置放置元素即可。先从 个位置选取 个位置放置第一个元素，再从剩下的 个位置取 个位置放置第二个元素，以此类推，可以得到下面的式子：

下面是数 的另一种描述。

定理4 元素集合的 有序划分（划分为 个集合后把所有子集视作不同元素进行排列 ）的数目为 其中 表示第 个子集有 个元素， 为划分得到的子集数目；而 无序划分的数目为

证明过程与定理3基本相同。

举个例子， 的 有序划分中的 与 是不同的划分。可以看作将这些元素放入了不同的盒子，无序划分则放入了相同的盒子里。

例1 在 的棋盘上放置 辆车，使得任意两辆车都不在同一直线或同一竖线上，那么放置的方法种数有 种；若这些车有 种且第 种车有 辆，那么放置的方法种数为 SOL 实际上是要找出 个序偶 的组合的个数，每一种组合的这些序偶的横纵坐标两两不等。车子都相同时，每一行只有一辆车，无需考虑顺序，于是可以直接假定坐标为 那么 实际上就是 的排列，于是总数目为 个。当车之间有差异时，车的集合相当于一个多重集合，相当于要对这些坐标（车子）根据它们之间的差异将进行排列，于是问题转化为多重集合的排列，最终答案就很显然了。

多重集合的组合（1）

多重集合 的 组合是 中 个对象的无序选择，选择的结果仍然是一些多重集合。

定理5 设 有 种元素且每种元素有无穷多个，那么 的 组合的个数为 PROOF 设 于是它的 组合是形如 的集合，满足 且 为非负整数。问题就转化为了不定方程 的非负整数解的组数问题了。下面证明该方程的非负整数解的组数为多重集合 的排列的个数（即长度为 且含有 个 和 个 的串）。给定 的一个排列，其中的 个 将这 个 分成了 部分¹ ，即从左到右分别有 个 它们显然满足 反之，若给定满足 的非负整数 把上述步骤倒推可以构造出 的一个排列；这就证得了该方程的非负整数解的组数为多重集合 的排列的个数。于是解的组数为

额，自己在做时搞出来一个没啥用的东西……

设从 种元素取出 个包含所有种类的元素的取法为 当第一种元素取出 个时，相当于要在剩下的 种元素取出 个元素且要包含剩下所有种类的元素，这个取法刚好是 且 于是 于是结果为 （化简不了……

后续的章节中将继续讨论不定方程 的解有上界时的解（解有下界时换个元即可）。

练习

1：确定性如 的塔状集的数目。

SOL 显然为